Strange Attractors

An attractor is a set of points described by a dynamical system. Some attractors exhibit chaotic behavior -- these strange attractors are often visually striking and intricate despite being described by simple mathematical expressions. Here are some colored visualizations, with brighter values indicating that the system spent more time in that area. Source code can be found here. This work is inspired partly by work done by Paul Bourke.

back to home
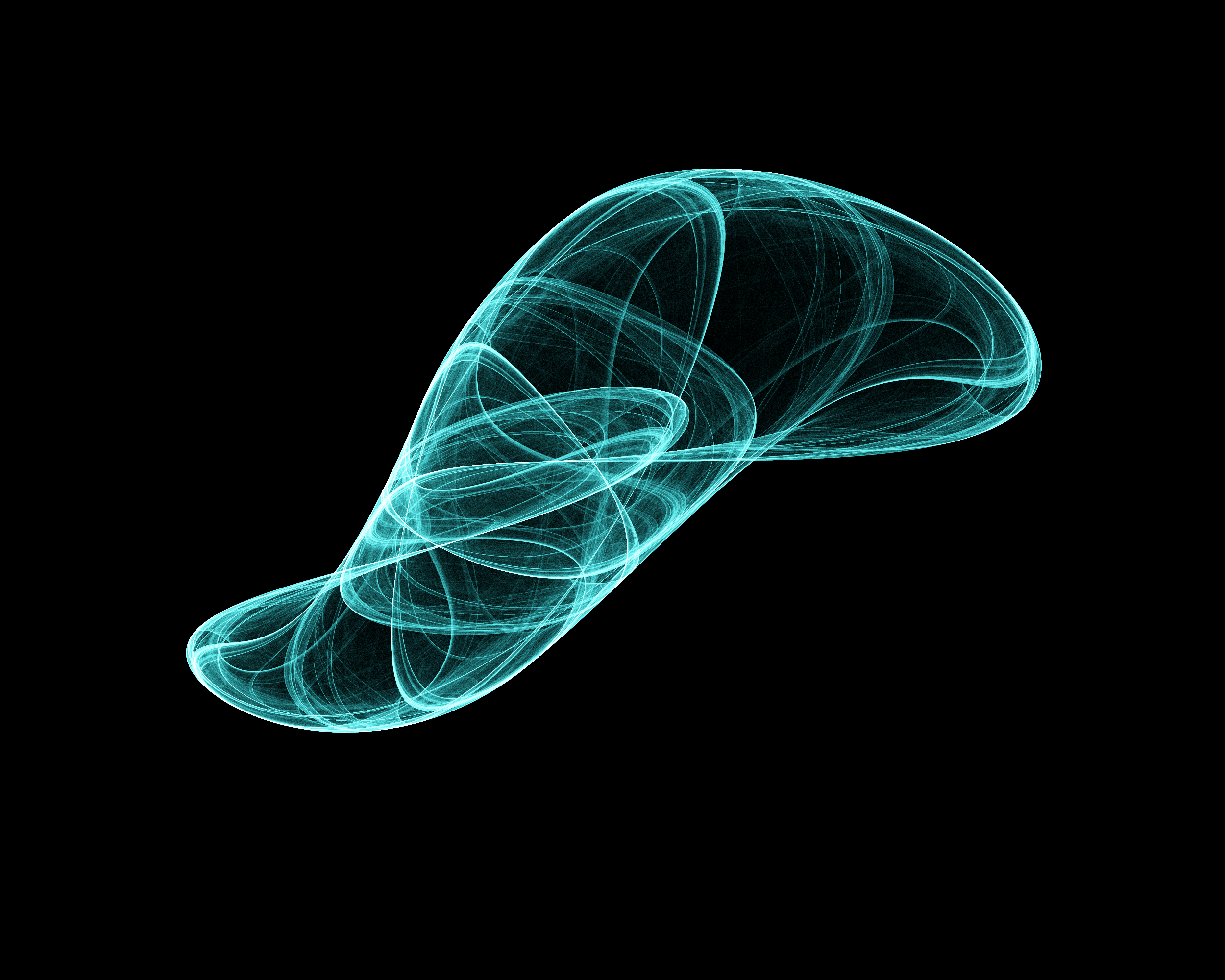
peterdejong Peter de Jong Attractor

$$\begin{eqnarray} x_{t + 1} = \sin{(a y_t)} - \cos{(b x_t)} \\ y_{t + 1} = \sin{(c x_t)} - \cos{(d y_t)} \end{eqnarray}$$

$$a=-0.709, b=1.638, c=0.452, d=1.740$$
thomas Thomas' Cyclically Symmetric Attractor

$$\begin{eqnarray} \frac{dx}{dt} &=& \sin{(y)} - bx \\ \frac{dy}{dt} &=& \sin{(z)} - by \\ \frac{dz}{dt} &=& \sin{(x)} - bz \\ \end{eqnarray}$$

$$b = 0.208186$$
3-doublescroll Generalized Chua's Circuit

$$\begin{eqnarray} \frac{dx}{dt} &=& \alpha (y - h(x)) \\ \frac{dy}{dt} &=& x - y + z \\ \frac{dz}{dt} &=& -\beta y - \gamma z \end{eqnarray}$$

$$\displaystyle h(x) = m_{2n - 1}x + \frac{1}{2}\sum_{k=1}^{2n-1}(m_{k-1} - m_k)(|x + b_k| - |x - b_k|)$$

For the 3-Double scroll attractor pictured:

$$\alpha=9, \beta=14.286, \gamma=0$$

$$m_0 = \frac{-1}{7}, m_1 = m_3 = m_5 = \frac{2}{7}, m_2 = m_4 = \frac{-4}{7}$$

$$b_1 = 1, b_2 = 2.15, b_3 = 3.6, b_4 = 8.2, b_5 = 13$$
aizawa Aizawa Attractor

$$\begin{eqnarray} \frac{dx}{dt} &=& (z - \beta) x - \delta y \\ \frac{dy}{dt} &=& \delta x - (z - \beta) y \\ \frac{dz}{dt} &=& \gamma + \alpha z - \frac{z^3}{3} - (x^2+y^2)(1 + \epsilon z) + \zeta z x^3 \end{eqnarray}$$

$$\alpha=0.95, \beta=0.7, \gamma=0.65, \delta=3.5, \epsilon=0.25, \zeta=0.1$$
clifford Clifford Attractor

$$\begin{eqnarray} x_{t + 1} &=& \sin{(a y_t)} + c \cos{(a x_t)} \\ y_{t + 1} &=& \sin{(b x_t)} + d \cos{(b y_t)} \\ \end{eqnarray}$$

$$a=-1.7, b=1.8, c=-1.9, d=-0.4$$

Pseudocode for Visualization 

            set initial conditions of system
            initialize 2D histogram for axes of choice
            until desired:
                propagate system dynamics
                increment system state in histogram
            for bin in 2D histogram:
                create pixel according to bin value
            display image